先月未完であった自力翻訳を終え、現在は見直し作業に入っています。
自力翻訳をしたのは、以下の明細書です。
US8233134B2
“Lithographic apparatus and device manufacturing method”
ASML Netherlands BV
(11,164ワード)
翻訳を再開する前に改めて明細書を読み直したところ、すでに終えた自分訳には読みにくい箇所が散見されました。訳し直しも考えましたが、今はその至らなさに向き合い、見直しを進めることにしました。
さて今回は、自力翻訳の過程で自分の理解が少しクリアになった話です。
露光技術における波長の短縮
半導体製造における露光工程では、マスクと呼ばれる原版を用いて光を照射し、パターンをウエハ上に転写します。パターンの微細化と集積度の向上のため、光源の短波長化が追求されてきました。
ArF(193nm)までは順調に短波長化が進みましたが、さらに短波長のEUV(波長:13.5nm)の技術的ハードルが高く、実用化には時間を要しました。その間、単純に短波長化するのではなく、既存のArF光源での露光技術をベースに、顕微鏡ですでに使用されていた「液浸」技術を応用し、見かけ上の波長を短縮し、短波長化と同様の効果を得る方法が採用されました。これが液浸露光です。
見かけ上の波長とは
液浸露光では、光源の波長自体は変えず、投影レンズとウエハとの間には屈折率の高い液体(例:超純水)を挟むことで「見かけ上の波長」を短縮します。
この「見かけ上の波長」については、以前ブログでも触れました。ただ、当時は「光源の波長は変わらないのに、なぜ媒質中で波長が短くなるのか」という点に納得しきれない部分がありますした。
特に、「見かけ上の波長が短くなる」と言われても、本当に波長が変化しているのか、それともそう見えるだけなのか? という点があいまいに感じていました。
光速の復習
真空中
真空中での光速cは、一定(3.00×108m/s)です。光速cは、波ひとつ分の長さである波長λ0と、単位時間当たりに通過する波の数である振動数fの積、としてあらわせます。
波長と振動数との関係:
光速c=λ 0×f(真空中の光の基本式)この式は、距離 ÷ 時間という見慣れた形と違うため少し違和感があったのですが、例えば、車のスピードを「タイヤの円周xタイヤの回転数(繰返しの回数)」としてあらわせるのと同じ考え方です。
媒質中
光速は、真空中で最大(最速)となりますが、屈折率(referactive index)により減速します。
屈折率nは、真空中の光速cを媒質中の光速vで割った値です。
屈折率n=真空の光速c/媒質中の光速v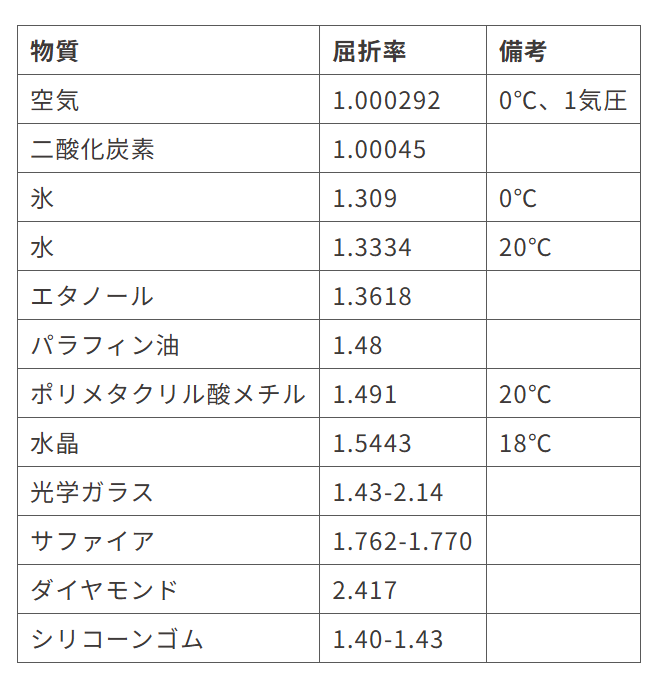
出典:αGEL
屈折率が大きいほど光速は遅くなります。媒質中の波長λは、次の式で表されます。
波長λ=真空の波長λ0/屈折率n振動数fは、媒質によって変わらず一定です。これは、異なる媒質の境界でも波が連続性を保つこと、または光のエネルギーがE=hf(hはプランク定数)で決まるためです。
つまり、媒質中の光速vは、以下のようにあらわせます。
媒質中の光速v=真空中の光速v/屈折率n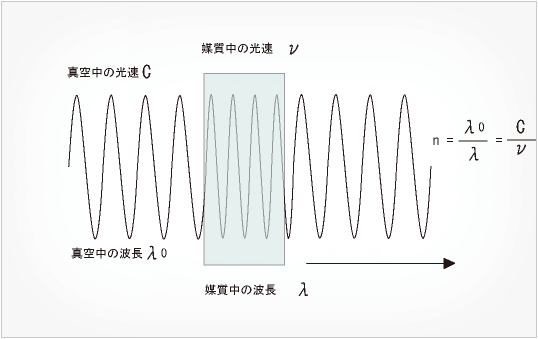
(出典:東海光学)
真空中・媒質中の光の波長変化を歩行に例える
真空中の光速は、舗装された道を歩く人の歩行スピードのようなものです。歩幅(波長)が広く、歩数(振動数)は一定です。
同じ人が砂場を歩く場合の歩行スピードはどうでしょう。
歩数(振動数)は一定ですが、砂に足を取られて歩幅(波長)は短くなり、その分歩行スピード(光速)が遅くなります。
このように、媒質中では光速が遅くなるため、波長が短くなって見える、つまり「見かけ上の波長」が短くなるのです。
今回こうした例えで考えることで、「見かけ上の波長」は媒質上で観察させる波長のことであり、光源の波長そのものが変化するわけではない、という点がより明確になりました。
まとめ
液浸露光では、屈折率の高い媒質を使うことで「見かけ上の波長」を短縮し、より微細なパターンの形成を可能にしています。
自分の説明を補強する調べ物をしていたら、すでに分かりやすくまとめられたサイトを見つけました。
こちらのサイトにあるように、光を擬人化するだけでなく、隊列と考えると、より屈折の理解がクリアになりますね。



コメント