液浸露光が微細化にどのように貢献するのかを理解するには、光が持つ基本的な性質とその振る舞いを知ることが必要です。本記事では、液浸露光の概要、光学的な基礎、そして臨界角の特性を中心に解説します。次の記事では、液浸露光の解像度向上における具体的なメカニズム(開口数や焦点深度の詳細)に焦点を当てます。
液浸露光(Immersion Lithography)とは
液浸露光は、従来の乾式リソグラフィ(dry lithography)に代わる解像度向上の技術です。投影レンズとウエハの間に高屈折率で透明度の高い液体(通常は超純水)を挟むことで、媒質中の見かけの短波長化を実現し、微細パターンの形成を可能にします。
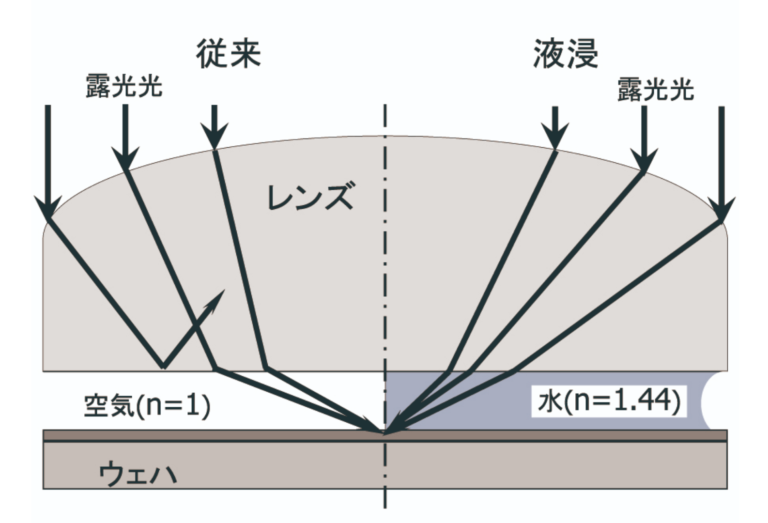
左側が従来の乾式露光、右側が液浸露光を示しています。
微細化アプローチのちがい
乾式露光のアプローチ
光の経路:光源 ⇒ マスク ⇒ 投影レンズ ⇒ (空気) ⇒ ウエハ
乾式露光では、主な微細化手段として、光源の波長を短縮するというアプローチが取られてきました。
- KrFエキシマレーザー(248 nm):初期の微細化技術。
- ArFエキシマレーザー(193 nm):さらなる微細化を実現。
- F2レーザー(157 nm):技術的・コスト的な限界に直面。
F2レーザー(157 nm)は、従来のレンズ材料(石英)がこの波長の光を吸収しやすく、CaF2(フッ化カルシウム)などの新材料の開発が必要となりました。しかし、この材料開発が技術的・コスト的な課題を伴ったため、実用化が困難となりました。
液浸露光のアプローチ
光の経路:光源 ⇒ マスク ⇒ 投影レンズ ⇒ 液体(液浸) ⇒ ウエハ
液浸露光では、光源の波長を短縮する代わりに、投影レンズとウエハの間の像形成空間での見かけの波長を短縮するというアプローチが取られました。
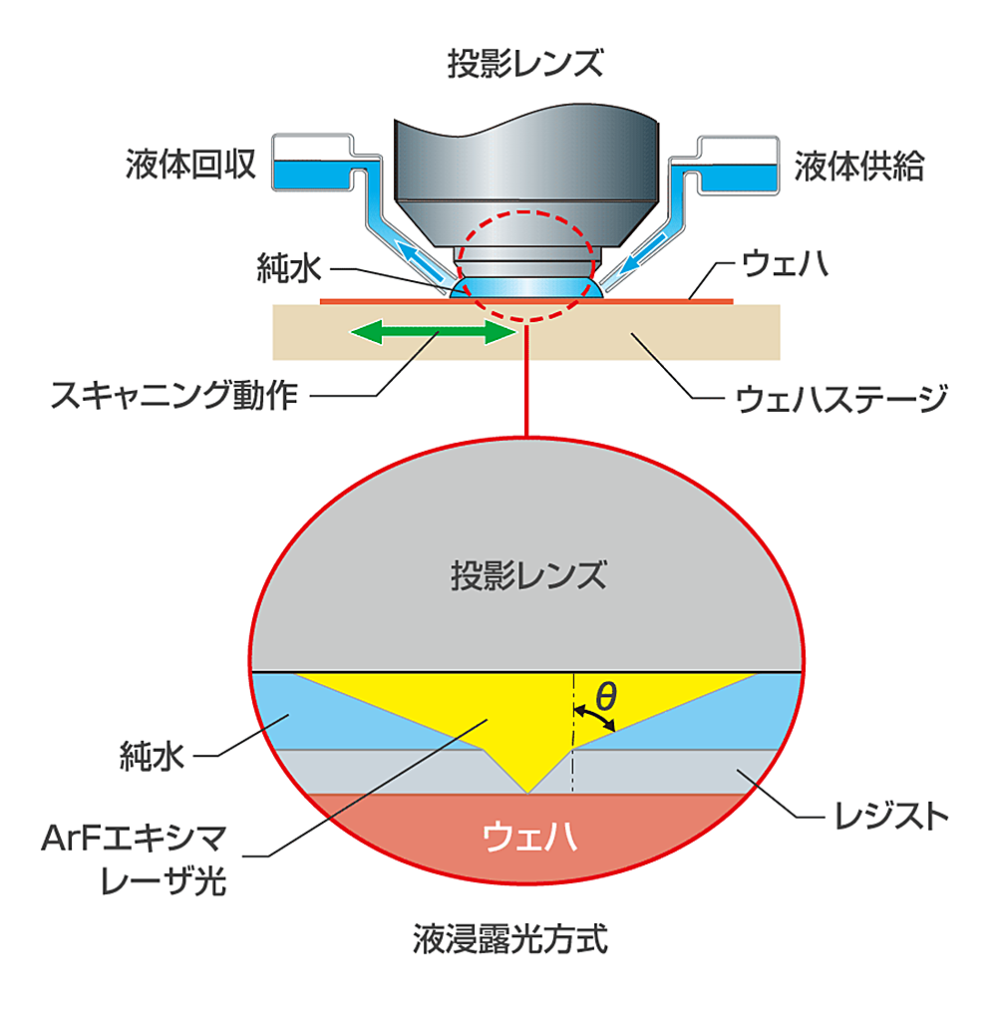
この見かけの波長については、媒質中での光の振る舞いが関係していますが、この光学原理については後ほど詳しく解説します。
液浸露光の光学原理
以下では、光の基本的な性質に立ち戻りつつ、液浸露光における原理をまとめます。
光の基本的な性質
光の性質は、波長λ、振動数ν、波の速さvによって特徴づけられ、次の関係式が成り立ちます。

波長λ ×振動数ν = 光の速さv
ここで重要なのは、振動数νが媒質の違いにかかわらず一定だという点です。振動数は光源の特性に依存し、媒質を変えても光が一秒間に振動する回数は変わりません。
真空中での光速
光速cは、真空中での光の速さを指します(約30万km/s)を指し、次の関係式が成り立ちます:
波長λ ×振動数ν =真空中での光速c
媒質中での光の速さ
光が媒質を進む際、その速さvは、媒質の屈折率nによって次のように変化します。:
媒質中での光の速さv = 真空中での光速c /媒質の屈折率n
屈折率nが大きいほど、光の進む速さvは遅くなります。
媒質中での波長の短縮
媒質中での光の速さ(v=c/n)を、光の基本式(λ×ν=v)に代入すると、波長λは次のように表せます。
λ ×ν = c/n ⇒λ=c/nν
- 媒質中での波長は、真空中の波長よりも短くなる、
- 屈折率nが大きいほど、波長は短くなる、
- 振動数νは媒質によらず一定なので、波長λの変化は、光の速さvの変化に依存する
ことが分かります。
ちなみに媒質中の波長λは、真空中の波長を用いて、λ=λ0/nとも表せ、屈折率nを媒質中の波長の縮小率として考えられます。
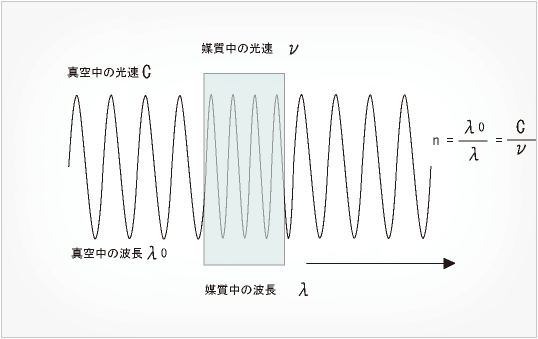
これは、上の波長λの式で真空中の波長を表すとλ0=c/vと表せることから、波長λの式に代入すると導けます。
媒質中での光の伝播
媒質中では光は波動として進み、媒質中の電子を振動させることでエネルギーを伝えます。この伝播の速さは、媒質の密度・分子構造に影響され、高密度で屈折率の高い媒質(例:水)では、光が進む速さは空気中よりも遅くなります(なお、空気中の屈折率は真空中とほぼ同一と見なします)。
見かけの波長とは?
先ほど、液浸露光では、「光源の波長を短縮する代わりに、投影レンズとウエハの間の像形成空間での見かけの波長を短縮する」と書きました。
なぜここで見かけの波長という表現が使われているのでしょうか。
液浸露光で利用するArFエキシマレーザーの波長は真空中で193 nmと決まっています。これはレーザー光が生成される際の振動数と真空中の光速から定まる値です。この振動数νは媒質が変わっても一定であるため、光源の波長そのものは変化しません。
しかし先ほど述べたように、媒質中ではその屈折率nにより光の速さが遅くなるために、媒質内で観察される波長は短くなります。この媒質中で観察される、という点が、見かけの波長、と言われるゆえんで、この媒質内で観察される波長が短くなったからといって、光そのものの波長(つまり、真空中での波長)が変わった訳ではありません。
なお媒質中の波長は先ほど記載したとおり、真空中の波長λ0を屈折率nで割って表すことができます。
屈折とスネルの法則
光が媒質を通過するとき、その進む速さと進む角度は媒質の屈折率に大きく影響されます。
この関係を理解する鍵が、屈折の法則として知られるスネルの法則です。
スネルの法則(Snell’s Law)とは
光が異なる媒質間を通過するとき、その進む角度は媒質の屈折率に基づいて変化します。これが屈折と呼ばれる現象で、スネルの法則(Snell’s Law)によって説明されます。
光が媒質の界面に入射する際、媒質1の屈折率(絶対屈折率:真空に対する)をn1、媒質2の屈折率をn2とした場合、入射角(θi)と屈折角(θr)の間には次の関係があります:
n1・sinθi=n2・sinθr
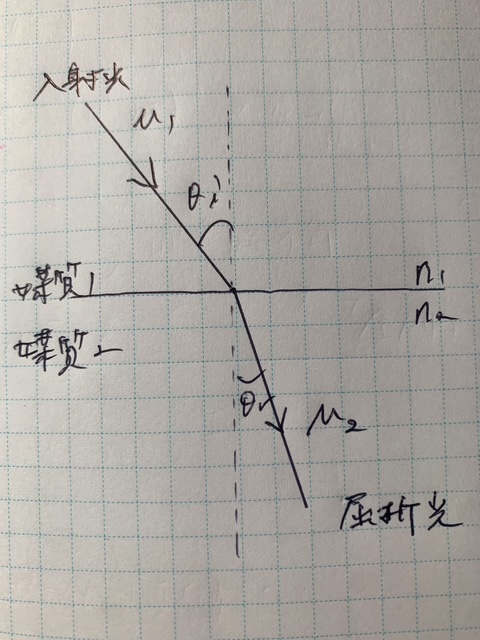
この式から、次のような関係が導かれます。
sinθi/sinθ=n1/n2=n12
n12 :媒質1(屈折率n1)に対する媒質2(屈折率n2)の相対屈折率
n1、n2:真空に対する媒質1、媒質2それぞれの絶対屈折率
さらに、屈折率は光速とも密接に関係しており、媒質1、媒質2中での光の速さをそれぞれv1、v2とすると、次の関係が成り立ちます:
n12=v1/v2
これは、屈折率が媒質中での光の速度比を表していることを意味します。
屈折率が高い媒質ほど光の速度は遅くなり、進む角度が大きく変化します。
臨界角と全反射
臨界角と全反射
臨界角とは、光が屈折せず全反射を始める際の入射角です。
具体的には、上の図のレンズ⇒空気、レンズ⇒水、のように、屈折角が大きい媒質から屈折角が小さい媒質に光が進むと、屈折角が90°に達することがあります。
このときの入射角を超えると、光は事実上屈折せず、すべて反射(全反射)するようになります。そのため露光においては、必臨界角がより広く取れる構造が、集光という観点から重要になってきます。
実際に手を動かしてみた
乾式露光と液浸露光における入射角や臨界角、全反射の様子を図解しました。ArFレーザーの室温における屈折率として
- レンズ(屈折率 1.5)
- 純水(屈折率 1.44)
- 空気(屈折率 1.00)
の条件で実際に三角関数表を参照しながら計算をすると
- 乾式露光(空気-レンズ)では、入射角は0°から41°で全反射を迎えること
- 液浸露光(純水-レンズ間)では、入射角は0°から74°で全反射を迎えること
が導けました。左側が乾式露光、右側が液浸露光です。赤色で塗った箇所から分かるように、乾式露光では許容できる入射光の範囲が狭く、液浸露光では臨界角が74°まで広がるため、許容できる入射光の範囲が広くなることが分かります。これによってウエハに到達可能な光の角度範囲が広がる、ということが視覚的に理解できました。
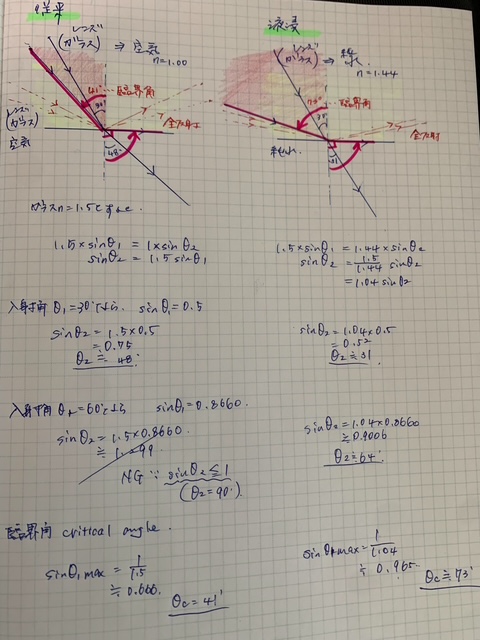
液浸露光と臨界角
液浸露光では、高屈折率の液体(水など)を用いることで臨界角を大きくし、より広い角度成分の光を収集可能にします。この特性により、ウエハに到達する光の範囲が広がり、より微細なパターン形成を可能にします。しかし、この仕組みだけでは解像度向上の全体を理解するのに不十分です。
次の記事では、液浸露光における開口数NA・解像度・焦点深度DOFという重要要素に触れ、開口数NAをどのように高めることで微細化が可能になるのかの理解をまとめます。



コメント